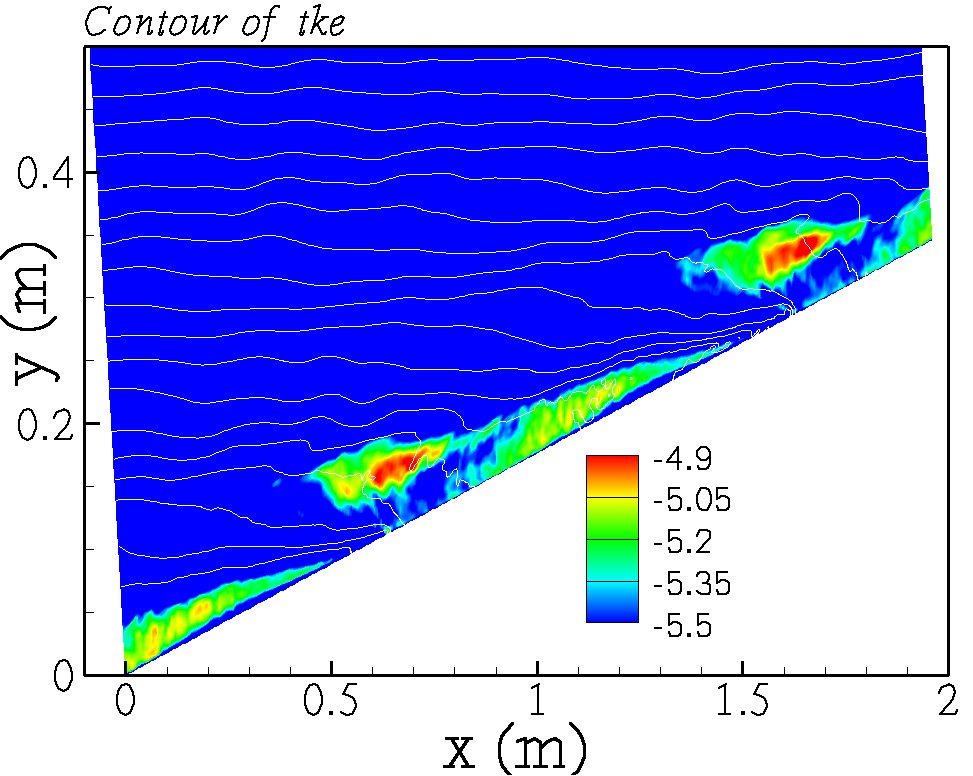
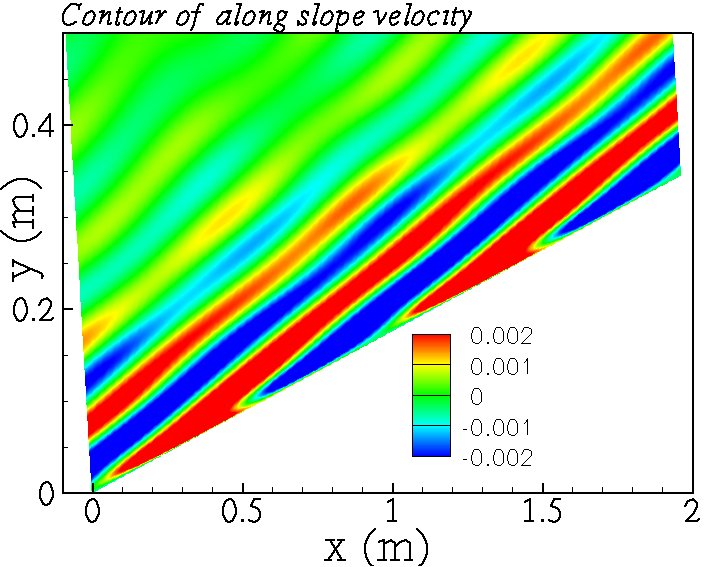
Direct numerical simulation is performed to study the internal gravity wave reflection on a sloping boundary, considering near critical slope angles. Our objective is to understand the role of near critical slopes in mixing near the boundaries during internal wave reflection. The wave field includes only the reflected wave, this is done by imposing velocity and density boundary conditions for the reflected wave at the sloping bottom. Two different scenarios have been considered, first by keeping slope angle constant and studying the effect of Froude number, second by keeping Froude number constant and varying the slope angle. With increasing Froude number, the reflection process becomes increasingly nonlinear with the formation of higher harmonics and subsequently fine scale turbulence. At a critical value of Froude number, turbulence is initiated via convective instability. Also, turbulent intensities are more pronounced for somewhat off-critical reflection compared to exactly critical reflection. As the Froude number increases, the near wall shear plays a dominant role in critical reflection by enhancing turbulence compared to off-critical reflection. For a fixed slope angle, as the Froude number increases the fraction of the input energy converted into the turbulent kinetic energy increases and saturates at higher Froude numbers.
 |
 |
| Contour of turbulent kinetic energy. | Contour of along slope velocity. |